Projectile Motion: Understanding the Equation of Trajectory

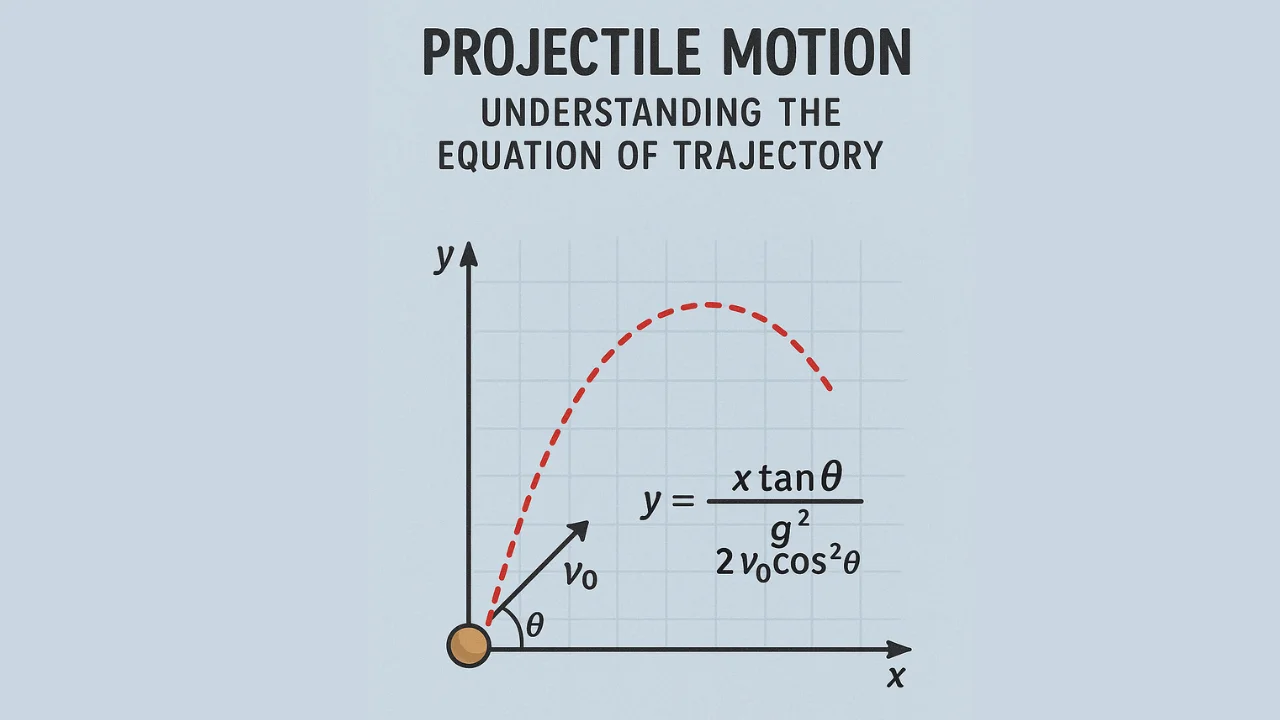
Projectile motion is a fundamental concept in physics that describes the motion of an object launched into the air and influenced only by gravity. The equation of trajectory in projectile motion helps predict the path (or trajectory) of the projectile. Whether you’re a student or an enthusiast, understanding this equation is crucial for solving real-world problems in mechanics, engineering, and ballistics.

What is the Equation of Trajectory in Projectile Motion?

The equation of trajectory represents the parabolic path followed by a projectile under the influence of gravity, neglecting air resistance. It is derived from the horizontal and vertical motion components and is given by:y=xtan⁡θ−gx22u2cos⁡2θy=xtanθ−2u2cos2θgx2​

Where:

• yy = vertical displacement
• xx = horizontal displacement
• θθ = angle of projection
• uu = initial velocity
• gg = acceleration due to gravity (9.8 m/s29.8m/s2)

This equation shows that the trajectory of a projectile is a parabola.

Derivation of the Equation of Trajectory

1. Horizontal Motion (x-axis):
   Since there is no acceleration in the horizontal direction (ignoring air resistance), the horizontal velocity remains constant:x=ucos⁡θ⋅tx=ucosθ⋅t
2. Vertical Motion (y-axis):
   The vertical motion is influenced by gravity, leading to acceleration gg downward:y=usin⁡θ⋅t−12gt2y=usinθ⋅t−21​gt2
3. Eliminating Time (t):
   From the horizontal motion equation, t=xucos⁡θt=ucosθx​. Substituting this into the vertical motion equation gives the trajectory equation:y=xtan⁡θ−gx22u2cos⁡2θy=xtanθ−2u2cos2θgx2​

Key Applications of the Trajectory Equation

• Sports Science: Calculating the optimal angle for maximum range in sports like javelin throw, football, or basketball.
• Military & Defense: Determining artillery shell trajectories for accurate targeting.
• Engineering: Designing roller coasters, water fountains, and other parabolic motion-based systems.
• Space Exploration: Predicting satellite and spacecraft motion in gravitational fields.

Factors Affecting Projectile Trajectory

1. Initial Velocity (uu): Higher velocity increases the range and height.
2. Angle of Projection (θθ): The maximum range is achieved at 45∘45∘ (in a vacuum).
3. Gravity (gg): Stronger gravity reduces the range and height.
4. Air Resistance: In real-world scenarios, drag force alters the trajectory.